
Autokorrelation är en statistisk metod som används för analyser av tidsserier. Syftet är att mäta korrelationen mellan två värden i samma datauppsättning vid olika tidsteg. Även om tidsdata inte används för att beräkna autokorrelation, bör dina tidsökningar vara lika för att få meningsfulla resultat. Autokorrelationskoefficienten tjänar två syften. Det kan upptäcka icke-slumpmässighet i en datauppsättning. Om värdena i datauppsättningen inte är slumpmässiga kan autokorrelation hjälpa analytiker att välja en lämplig tidsseriemodell.
Beräkna medelvärdet eller genomsnittet för de data du analyserar. Medelvärdet är summan av alla datavärden dividerat med antalet datavärden (n).
Bestäm en tidsfördröjning (k) för din beräkning. Fördröjningsvärdet är ett heltal som anger hur många tidssteg som skiljer ett värde från ett annat. Till exempel är fördröjningen mellan (y1, t1) och (y6, t6) fem, eftersom det finns 6 - 1 = 5 tidssteg mellan de två värdena. När du testar för slumpmässighet beräknar du vanligtvis bara en autokorrelationskoefficient med fördröjning k = 1, även om andra fördröjningsvärden också fungerar. När du bestämmer en lämplig tidsseriemodell måste du beräkna en serie autokorrelationsvärden med hjälp av ett annat fördröjningsvärde för varje.
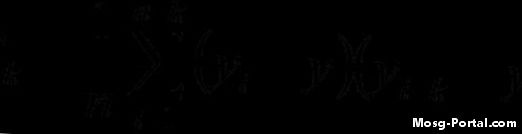
Beräkna autokovariansfunktionen med den angivna formeln. Till exempel, beräknade du den tredje iterationen (i = 3) med en fördröjning k = 7, då beräkningen för den iterationen skulle se ut så här: (y3 - y-bar) (y10 - y-bar) Iterera genom alla värden på "i" och sedan ta summan och dela den med antalet värden i datauppsättningen.
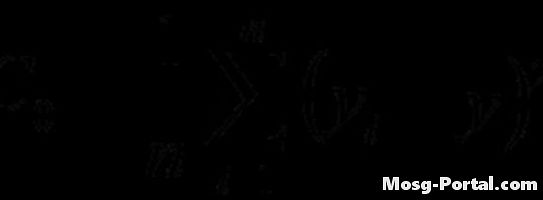
Beräkna variansfunktionen med den angivna formeln. Beräkningen liknar den för autokovariansfunktionen, men fördröjning används inte.

Dela autokovariansfunktionen med variansfunktionen för att få autokorrelationskoefficienten. Du kan kringgå detta steg genom att dela formlerna för de två funktionerna som visas, men många gånger behöver du autokovarians och varians för andra ändamål, så det är praktiskt att beräkna dem också individuellt.