Laws of Pendulum Motion

Innehåll

• TL; DR (för lång; läste inte)
• Enkel harmonisk rörelse
• Lagar om en enkel pendel
• Enkelt pendel derivation
• Faktorer som påverkar pendelrörelsen
• Exempel på pendelens längd
• Enkel pendeldefinition
• Newtons lagar i pendlar

Pendlar har intressanta egenskaper som fysiker använder för att beskriva andra föremål. Till exempel följer planetbanan ett liknande mönster och att svänga på ett svängset kan känna att du är på en pendel. Dessa egenskaper kommer från en serie lagar som styr pendelens rörelse. Genom att lära dig dessa lagar kan du börja förstå några av de grundläggande principerna för fysik och rörelse i allmänhet.

TL; DR (för lång; läste inte)

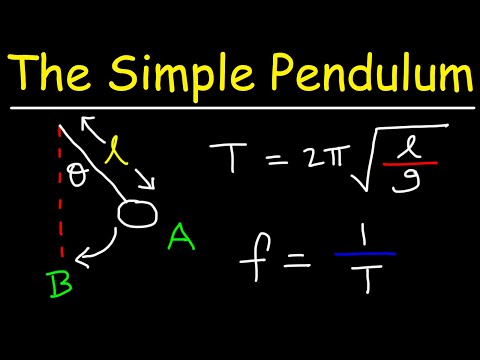
Rörelsen hos en pendel kan beskrivas med hjälp av θ (t) = θ_maxcos (2πt / T) i vilken θ representerar vinkeln mellan strängen och den vertikala linjen i mitten, t representerar tid och T är perioden, den tid som krävs för att en fullständig cykel av pendelrörelsen ska ske (uppmätt med 1 / f) av förslaget till en pendel.

Enkel harmonisk rörelse

Enkel harmonisk rörelse, eller rörelse som beskriver hur en objekthastighet svänger proportionellt mot mängden förskjutning från jämvikt, kan användas för att beskriva ekvationen för en pendel. En pendelbobsvängning hålls i rörelse av denna kraft som verkar på den när den rör sig fram och tillbaka.

••• Syed Hussain Ather

Lagarna som styr pendelrörelsen ledde till upptäckten av en viktig egenskap. Fysiker bryter upp krafter i en vertikal och en horisontell komponent. I pendelrörelse tre krafter arbetar direkt på pendeln: massan på bob, tyngdkraften och spänningen i strängen. Massa och tyngdkraft fungerar båda vertikalt nedåt. Eftersom pendeln inte rör sig upp eller ner, avbryter den vertikala komponenten i strängspänningen massan och tyngdkraften.

Detta visar att massan av en pendel inte har någon relevans för dess rörelse, men den horisontella strängspänningen gör det. Enkel harmonisk rörelse liknar cirkulär rörelse. Du kan beskriva ett objekt som rör sig i en cirkulär bana som visas i figuren ovan genom att bestämma vinkeln och radien det tar i motsvarande cirkulär bana. Sedan kan du hitta ekvationer med hjälp av trigonometri för den högra triangeln mellan cirkelns centrum, objektets position och förskjutningen i båda riktningarna x och y x = rsin (θ) och y = rcos (θ).

Den endimensionella ekvationen för ett objekt i enkel harmonisk rörelse ges av x = r cos (ωt). Du kan ytterligare ersätta EN för r i vilken EN är amplitud, den maximala förskjutningen från objektets initiala position.

Vinkelhastigheten ω med avseende på tid t för dessa vinklar θ ges av θ = ωt. Om du ersätter ekvationen som relaterar vinkelhastigheten till frekvensen f, ω = 2πf_, du kan föreställa dig denna cirkulära rörelse, då, som en del av en pendel som svänger fram och tillbaka, är den resulterande enkla harmoniska rörelseekvationen _x = A cos (2πft).

Lagar om en enkel pendel

••• Syed Hussain Ather

Pendlar, som massor på en fjäder, är exempel på enkla harmoniska oscillatorer: Det finns en återställningskraft som ökar beroende på hur förskjuten pendeln är, och deras rörelse kan beskrivas med hjälp av enkel harmonisk oscillatorekvation θ (t) = θ_maxcos (2πt / T) i vilken θ representerar vinkeln mellan strängen och den vertikala linjen i mitten, t representerar tid och T är period, den tid som krävs för att en fullständig cykel av pendelrörelsen ska ske (uppmätt med 1 / f) av förslaget till en pendel.

θ_max är ett annat sätt att definiera det maximala vinkeln som oscillerar under pendelrörelsen och är ett annat sätt att definiera pendelens amplitud. Detta steg förklaras nedan under avsnittet "Enkel pendeldefinition."

En annan implikation av lagarna i en enkel pendel är att svängningsperioden med konstant längd är oberoende av objektets storlek, form, massa och material på strängens ände. Detta visas tydligt genom det enkla pendulderivatet och ekvationerna som resulterar.

Enkelt pendel derivation

Du kan bestämma ekvationen för a enkel pendel, definitionen som beror på en enkel harmonisk oscillator, från en serie steg som börjar med rörelsekvationen för en pendel. Eftersom tyngdkraften hos en pendel är lika med pendelrörelsens kraft kan du ställa dem lika med varandra genom att använda Newtons andra lag med en pendelmassa M, stränglängd L, vinkel θ, gravitationsacceleration g och tidsintervall t.

••• Syed Hussain Ather

Du sätter Newtons andra lag som är lika med tröghetsmomentet I = mr²_ för lite massa _m och radie för cirkulär rörelse (längden på strängen i detta fall) r gånger vinkelaccelerationen α.

Det finns andra sätt att göra ett enkelt pendelderivat. Förstå innebörden bakom varje steg för att se hur de är relaterade. Du kan beskriva en enkel pendelrörelse med hjälp av dessa teorier, men du bör också ta hänsyn till andra faktorer som kan påverka enkel pendelteori.

Faktorer som påverkar pendelrörelsen

Om du jämför resultatet av denna härledning θ (t) = θ_maxcos (t (L / g)²) till ekvationen av en enkel harmonisk oscillator (_θ (t) = θ_maxcos (2πt / T)) b_y att ställa in dem lika med varandra, du kan härleda en ekvation för perioden T.

Lägg märke till att denna ekvation T = 2π (L / g)^-1/2 beror inte på massan M av pendeln, amplituden θ_max, inte heller på tiden t. Det betyder att perioden är oberoende av massa, amplitud och tid, men istället förlitar sig på strängens längd. Det ger dig ett kortfattat sätt att uttrycka pendelrörelser.

Exempel på pendelens längd

Med ekvationen under en period T = 2π (L / g) __^-1/2, kan du ordna om ekvationen för att erhålla L = (T / 2_π)² / g_ och ersätt 1 sek för T och 9,8 m / s² för g för att uppnå L = 0,0025 m. Tänk på att dessa ekvationer av enkel pendelteori antar att strängens längd är friktionsfri och masslös. För att ta hänsyn till dessa faktorer krävs mer komplicerade ekvationer.

Enkel pendeldefinition

Du kan dra pendeln bakåt θ att låta den svänga fram och tillbaka för att se den svänga precis som en fjäder kan. För en enkel pendel kan du beskriva den med hjälp av rörelseekvationer för en enkel harmonisk oscillator. Rörelsekvationen fungerar bra för mindre vinkelvärden och amplitud, den maximala vinkeln, eftersom den enkla pendelmodellen förlitar sig på approximationen som sin (θ) ≈ θ för viss pendelvinkel θ. Eftersom värdena vinklar och amplituder blir större än ungefär 20 grader, fungerar inte denna approximation också.

Testa det själv. En pendel som svänger med en stor initial vinkel θ kommer inte att svänga så regelbundet så att du kan använda en enkel harmonisk oscillator för att beskriva den. Vid en mindre initial vinkel θpendeln närmar sig en regelbunden oscillerande rörelse mycket lättare. Eftersom massan av en pendel inte har någon betydelse för dess rörelse, har fysiker bevisat att alla pendlar har samma period för svängningsvinklar - vinkeln mellan pendelns centrum vid sin högsta punkt och pendelens mitt i dess stoppade läge - mindre än 20 grader.

För alla praktiska ändamål för en pendel i rörelse kommer pendeln till slut att retardera och stoppas på grund av friktionen mellan strängen och dess fästpunkt ovan såväl som på grund av luftmotstånd mellan pendeln och luften runt den.

För praktiska exempel på pendelrörelse beror period och hastighet på den använda materialtyp som skulle orsaka dessa exempel på friktion och luftmotstånd. Om du gör beräkningar på teoretiskt pendeloscillatoriskt beteende utan att redovisa dessa krafter, kommer det att stå för en pendel som oscillerar oändligt.

Newtons lagar i pendlar

Newtons första lag definierar objektets hastighet som svar på krafter. Lagen säger att om ett föremål rör sig med en specifik hastighet och i en rak linje, kommer det att fortsätta att röra sig med den hastigheten och i en rak linje, oändligt, så länge ingen annan kraft verkar på den. Föreställ dig att kasta en boll rakt framåt - bollen skulle gå runt jorden om och om om luftmotstånd och tyngdkraft inte verkade på den. Denna lag visar att eftersom en pendel rör sig sida vid sida och inte upp och ner har den inga upp och ner krafter som verkar på den.

Newtons andra lag används för att bestämma nettokraften på pendeln genom att ställa in tyngdkraften lika med kraften hos strängen som drar tillbaka upp på pendeln. Om du ställer in dessa ekvationer lika med varandra kan du härleda rörelsekvationerna för pendeln.

Newtons tredje lag säger att varje handling har en reaktion av lika kraft. Denna lag fungerar med den första lagen som visar att även om massan och tyngdkraften avbryter den vertikala komponenten i strängspänningsvektorn, ingenting avbryter den horisontella komponenten. Denna lag visar att krafterna som verkar på en pendel kan avbryta varandra.

Fysiker använder Newtons första, andra och tredje lag för att bevisa den horisontella strängspänningen flyttar pendeln utan hänsyn till massa eller tyngdkraft. Lagarna i en enkel pendel följer idéerna i Newtons tre rörelseregler.