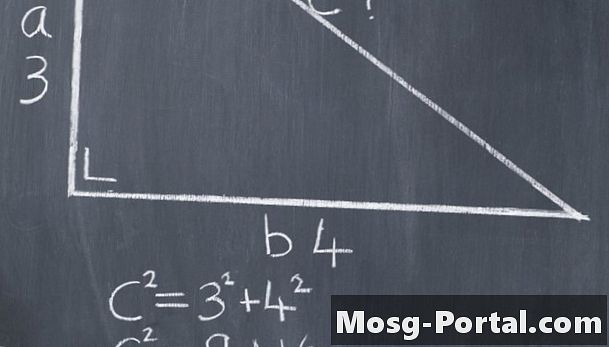
Innehåll
En hypotenuse är den längsta sidan av en höger triangel. Det är den sida som är direkt motsatt från rätt vinkel, och eleverna börjar först lära sig den här termen i geometri under mellanstadiet. Du kan hitta längden om de ges antingen de andra två sidorna av triangeln, eller ett vinkelmått och en sidolängd.
Pythagoras sats
I en höger triangel kallas de två sidorna som skapar 90-graders vinkel ben, och den långa sidan som förbinder dem kallas hypotenusen. Du kan hitta längden på hypotenusen från två ben eller ett ben och ett vinkelmått. Pythagorean Theorem är en formel som används för att hitta längden på någon av sidorna på en höger triangel när de ges två sidor. Formeln uttrycks vanligtvis som a ^ 2 + b ^ 2 = c ^ 2, där a och b är benen, och c är hypotenusen. Om du får a och b kan du använda dem och en viss algebra för att hitta längden på hypotenusen. Oavsett variabel som markerar hypotenusen, kommer den sidan att vara c i Pythagorean Theorem formel.
Koppla in den
För att lösa ett rätt triangelproblem måste du alltid hitta den saknade sidan av en triangel med hjälp av de andra två sidorna. För att hitta hypotenusen, anslut värdena för a och b. Titta till exempel på en triangel med sidolängder på 3 och 4. Om du ansluter dem till formeln, 3 ^ 2 + 4 ^ 2 = c ^ 2, och förenklar får du 9 + 16 = c ^ 2. Att lägga till 9 + 16 ger dig 25 = c ^ 2.
Lös ekvationen
När du har kvadrat benen och lagt dem ihop måste du fortfarande få c av sig själv. För att få en variabel i sig själv i en ekvation, använd kardinalregeln för algebra: vad du än gör på ena sidan av ekvationen, gör du också på den andra. I det här fallet behöver du "c" helt av sig själv, eftersom det är längden på hypotenusen. Om du tar kvadratroten på 25 ger du kvadratroten av c ^ 2: c = 5.
Trippel trianglar
Pythagorean Triples är rätt trianglar som har heltalvärden för varje sida och kan användas för att hitta hypotenusen för vissa trianglar utan att göra några beräkningar. Det finns många olika tripplar, men de vanligaste är 3-4-5 och 5-12-13 trianglar. Dessa sidolängder kan vara faktorer i större trianglar, men de kommer alltid att minska till en jämn trippel. Om du till exempel har benlängder på 10 och 24 kan du ansluta dem till ekvationen och ta kvadratroten 10 ^ 2 + 24 ^ 2. Men om du känner till dina tripplar, noterar du att 10 och 24 är två gånger 5 och 12, så hypotenusen måste vara två gånger 13 eller 26.