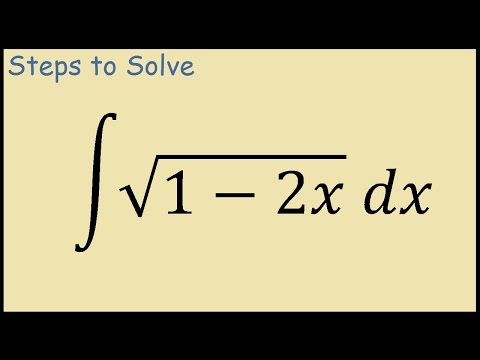
Innehåll
- Integration av grundläggande fyrkantiga rotfunktioner
- Integration av mer komplexa fyrkantiga rotfunktioner
Integrera funktioner är en av kärnanvändningarna för kalkylen. Ibland är detta enkelt, som i:
F (x) = ∫ (x3 + 8) dx
I ett jämförelsevis komplicerat exempel av denna typ kan du använda en version av grundformeln för att integrera obestämda integraler:
∫ (xn + A) dx = x(n + 1)/ (n + 1) + An + C,
där A och C är konstanter.
Således för detta exempel,
∫ x3 + 8 = x4/ 4 + 8x + C.
Integration av grundläggande fyrkantiga rotfunktioner
På ytan är det besvärligt att integrera en kvadratrotfunktion. Till exempel kan du bli stymied av:
F (x) = ∫ √dx
Men du kan uttrycka en kvadratrot som en exponent, 1/2:
√ x3 = x3(1/2) = x(3/2)
Integralen blir därför:
∫ (x3/2 + 2x - 7) dx
som du kan använda den vanliga formeln ovan:
= x(5/2)/ (5/2) + 2 (x2/ 2) - 7x
= (2/5) x(5/2) + x2 - 7x
Integration av mer komplexa fyrkantiga rotfunktioner
Ibland kan du ha mer än en term under det radikala tecknet, som i detta exempel:
F (x) = ∫ dx
Du kan använda u-substitution för att fortsätta. Här ställer du u lika med mängden i nämnaren:
u = √ (x - 3)
Lös detta för x genom att kvadratera båda sidorna och subtrahera:
u2 = x - 3
x = u2 + 3
Detta gör att du kan få dx i termer av u genom att ta derivatet av x:
dx = (2u) du
Att ersätta tillbaka i den ursprungliga integralen ger
F (x) = ∫ (u2 + 3 + 1) / udu
= ∫du
= ∫ (2u2 + 8) du
Nu kan du integrera detta med hjälp av den grundläggande formeln och uttrycka u i termer av x:
∫ (2u2 + 8) du = (2/3) u3 + 8u + C
= (2/3) 3 + 8 + C
= (2/3) (x - 3)(3/2) + 8 (x - 3)(1/2) + C