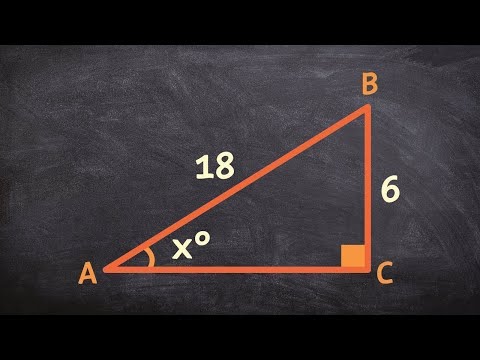
Trigonometri är studiet av trianglar, specifikt att mäta deras sidor och vinklar. Det finns några lätt att komma ihåg regler för att bestämma vinklar i en cinch, till exempel det faktum att summan av den inre vinkeln i en triangel är 180 grader. Trigonometri handlar om beräkningen av vinklar snarare än att mäta dem med en gradskiva, även om det vanligtvis finns minst en mätning som måste göras, vare sig det är en sida av en triangel eller en av de inre vinklarna.
Bestäm vilken typ av triangel som innehåller vinkeln du försöker hitta. Detta kan vara en liksidig triangel, som har tre lika vinklar att gå med sina tre lika sidor; en likbenad triangel, som har två lika sidor och två lika vinklar; en höger triangel, som har en 90-graders vinkel och två spetsiga vinklar; eller en oregelbunden triangel, som har tre ojämna vinklar.
Rita en linje från en av de andra vinklarna i triangeln så att den korsar motsatt sida i rätt vinkel.
Mät sidan av den högra triangeln mellan rätt vinkel och vinkeln du försöker hitta. Detta kallas den intilliggande sidan av triangeln.
Mät sidan av triangeln från den vinkel du försöker hitta till den andra spetsiga vinkeln i triangeln. Detta kallas hypotenusen.
Utvärdera den omvända kosinus förhållandet mellan den intilliggande sidan till hypotenusen med en vetenskaplig kalkylator. Den omvända kosinusfunktionen på kalkylatorn är märkt "cos¯¹". Detta ger dig vinkeln i grader eller radianer, beroende på hur din vetenskapliga kalkylator är konfigurerad. Till exempel, om den intilliggande sidan är 1 och hypotenusen är 2, beräknar du den omvända kosinus på 1/2. Använd din vetenskapliga kalkylator för att hitta den omvända kosinus på 1/2: cos¯¹ (1/2) = 60 grader.