En liksidig triangel är en triangel med alla tre sidor av samma längd. Ytan på en tvådimensionell polygon, såsom en triangel, är den totala arean som finns i sidorna på polygonen. De tre vinklarna på en liksidig triangel är också lika stora i den euklidiska geometri. Eftersom det totala måttet på vinklarna i en euklidisk triangel är 180 grader, betyder detta att vinklarna på en liksidig triangel alla mäter 60 grader. Ytan på en liksidig triangel kan beräknas när längden på en av dess sidor är känd.

Bestäm området för en triangel när basen och höjden är kända. Ta alla två identiska trianglar med bas och höjd h. Vi kan alltid bilda ett parallellogram av baser och höjd h med dessa två trianglar. Eftersom området för ett parallellogram är s x h är arean A för en triangel därför ½ s x h.

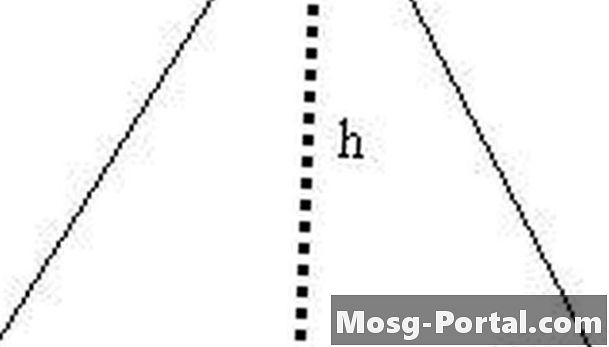
Forma den liksidiga triangeln i två högra trianglar med linjesegmentet h. Hypotenusen på en av dessa högra trianglar längd s, en av benen har längd h och den andra benen har längd s / 2.
Express h i termer av s. Med hjälp av den högra triangeln som bildas i steg 2, vet vi att s ^ 2 = (s / 2) ^ 2 + h ^ 2 med Pythagorean-formeln. Därför h ^ 2 = s ^ 2 - (s / 2) ^ 2 = s ^ 2 - s ^ 2/4 = 3s ^ 2/4, och vi har nu h = (3 ^ 1/2) s / 2.
Byt ut värdet på h erhållet i steg 3 i formeln för ett triangelområde som erhållits i steg 1. Eftersom A = ½ sxh och h = (3 ^ 1/2) s / 2 har vi nu A = ½ s (3 ^ 1/2) s / 2 = (3 ^ 1/2) (s ^ 2) / 4.
Använd formeln för area av en liksidig triangel som erhållits i steg 4 för att hitta arean för en liksidig triangel med sidor med längd 2. A = (3 ^ 1/2) (s ^ 2) / 4 = (3 ^ 1/2 ) (2 ^ 2) / 4 = (3 ^ 1/2).