Innehåll
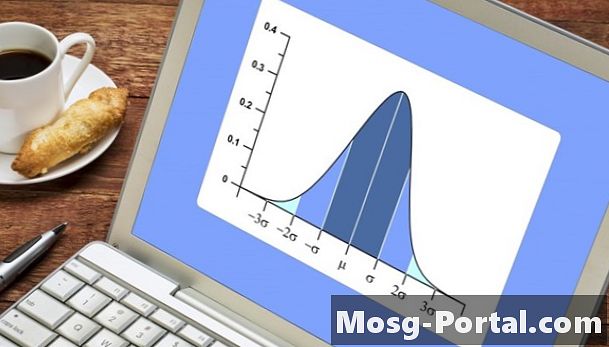
Efter att ha gjort en undersökning eller samlat in numeriska data om en population måste resultaten analyseras för att hjälpa dig dra slutsatser. Du vill veta parametrar som det genomsnittliga svaret, hur varierade svaren var och hur svaren är fördelade. En normalfördelning innebär att när de plottas skapar data en klockkurva som är centrerad på det genomsnittliga svaret och svansar av lika i både positiva och negativa riktningar. Om data inte är centrerade på genomsnittet och en svans är längre än den andra, är fördelningen av data sned. Du kan beräkna mängden skev i data med hjälp av medelvärdet, standardavvikelsen och antalet datapunkter.
Beräkna befolkningens skevhet
Lägg till alla värden i datauppsättningen och dela med antalet datapunkter för att få medelvärdet eller medelvärdet. För detta exempel kommer vi att anta en datauppsättning som innehåller svar från en hel population: 2, 4, 5, 7, 8, 10, 11, 25, 26, 27, 36. Denna uppsättning har ett medelvärde på 14,6.
Beräkna standardavvikelsen för datauppsättningen genom att kvadratera skillnaden mellan varje datapunkt och medelvärdet, lägga till alla dessa resultat, sedan dela med antalet datapunkter och slutligen ta kvadratroten. Vår datauppsättning har en standardavvikelse på 11,1.
Hitta skillnaden mellan varje datapunkt och medelvärdet, dela med standardavvikelsen, kubet det numret och lägg sedan till alla dessa nummer för varje datapunkt. Detta är lika med 6,79.
Beräkna befolkningens skevhet genom att dela 6,79 med det totala antalet datapunkter. Befolkningens skevhet för detta exempel är 0,617.
Beräkna provskehet
Beräkna medel- och standardavvikelsen från en datamängd som endast är ett urval av hela befolkningen. Vi kommer att använda samma datauppsättning som det föregående exemplet med medelvärdet 14.6 och standardavvikelsen 11.1, förutsatt att dessa siffror endast är ett urval av en större population.
Hitta skillnaden mellan varje datapunkt och medelvärdet, kubet det numret, lägg till varje resultat och dela sedan med kuben för standardavvikelsen. Detta är lika med 5,89.
Beräkna provskedja genom att multiplicera 5,89 med antalet datapunkter, dividerat med antalet datapunkter minus 1, och delas igen med antalet datapunkter minus 2. Provskydd för detta exempel skulle vara 0,720.