
Innehåll
Elektriska kretsar kan ha sina kretselement anordnade i antingen serier eller parallella. I seriekretsar är element anslutna med samma gren som s elektrisk ström genom var och en av dem en-för-en. I parallella kretsar har elementen sina egna separata grenar. I dessa kretsar kan strömmen ta olika vägar genom hela.
Eftersom strömmen kan ta olika vägar i en parallellkrets är strömmen inte konstant genom en parallellkrets. I stället för grenar som är anslutna parallellt med varandra är spänningen eller potentialfallet över varje gren konstant. Detta beror på att strömmen fördelar sig över varje gren i mängder som är omvänt proportionella mot motståndet för varje gren. Detta gör att strömmen är störst där motståndet är minst och vice versa.
Dessa egenskaper låter parallella kretsar tillåta laddning att flöda genom två eller flera vägar, vilket gör det till en standardkandidat i hem och elektriska apparater genom ett stabilt och effektivt kraftsystem. Den låter el flyta genom andra delar av en krets när en del är skadad eller trasig, och de kan fördela kraft lika över olika byggnader. Dessa egenskaper kan demonstreras genom ett diagram och ett exempel på en parallell krets.
Parallell Circuit Diagram
tips
Exempel på parallella kretsar
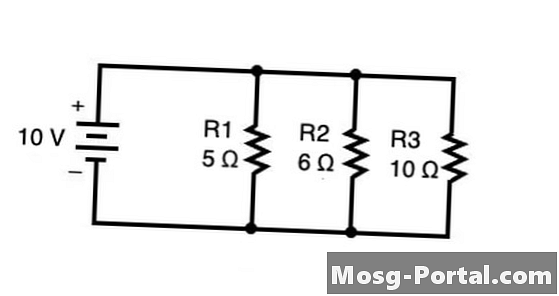
Använd formeln för att hitta det totala motståndet för motstånd anordnade parallellt med varandra 1 / Rtotal = 1 / R1 + 1 / R2 + 1 / R3 + ... + 1 / Rn där motståndet för varje motstånd summeras på höger sida av ekvationen. I ovanstående diagram kan det totala motståndet i ohm (Ω) beräknas enligt följande:
Observera att du bara kan "vända" på båda sidor av ekvationen från steg 3 till steg 4 när det bara finns en term på båda sidorna av ekvationen (i detta fall, 1 / Rtotal till vänster och 14/30 Ω till höger).
När du har beräknat motståndet kan ström och spänning beräknas med Ohms Law V = I / R i vilken V är spänning mätt i volt, jag är ström mätt i ampere, och R är motstånd i ohm. I parallella kretsar är summan av strömmarna genom varje bana den totala strömmen från källan. Strömmen vid varje motstånd i kretsen kan beräknas genom att multiplicera spänningstidernas motstånd för motståndet. Spänningen förblir konstant i hela kretsen så spänningen är batteriets eller spänningskällans spänning.
Parallell vs. seriekrets
••• Syed Hussain AtherI seriekretsar är strömmen konstant i hela, spänningsfall beror på motståndet för varje motstånd och det totala motståndet är summan av varje enskilt motstånd. I parallella kretsar är spänningen konstant genom, strömmen beror på varje motstånd och det inversa av det totala motståndet är summan av inversen för varje enskilt motstånd.
Kondensatorer och induktorer kan användas för att ändra laddningen i serie- och parallella kretsar över tid. I en seriekrets är det totala kapacitans av kretsen (ges av variabeln C), potentialen hos en kondensator att lagra laddning över tid, är den omvända summan av inverserna för varje enskild kapacitans, och total induktans (jag), induktorernas kraft att avge laddning över tid är summan av varje induktor. Däremot är den totala kapacitansen i en parallell krets summan av varje enskild kondensator, och det inverse av den totala induktansen är summan av inverserna för varje individuell induktans.
Serier och parallella kretsar har också olika funktioner. I en seriekrets, om en del är trasig, kommer strömmen inte att strömma genom kretsen alls. I en parallellkrets stoppar en enskild grenöppning endast strömmen i den grenen. Resten av grenarna fortsätter att fungera eftersom strömmen har flera vägar som den kan ta över kretsen.
Parallell serie

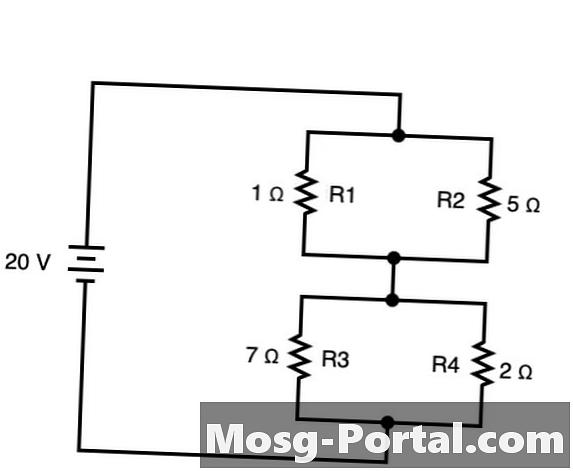
Kretsar som har båda grenade element som också är anslutna så att strömmen flyter i en riktning mellan dessa grenar både serie och parallell. I dessa fall kan du tillämpa regler från både serier och parallell efter behov. I exemplet ovan, R1 och R2 är parallellt med varandra att bilda R5och det är de också R3 och R4 att forma R6. De kan summeras parallellt enligt följande:
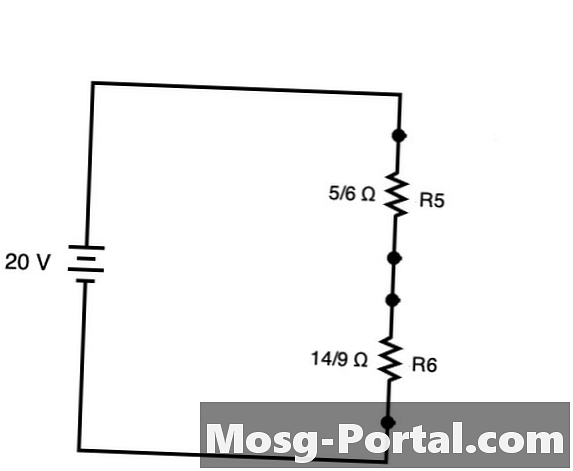
Kretsen kan förenklas för att skapa den krets som visas direkt ovan med R5 och R6. Dessa två motstånd kan läggas till direkt som om kretsen var serie.
Rtotal = 5/6 Ω + 14/9 Ω = 45/54 Ω + 84/54 Ω = 129/54 Ω = 43/18 Ω eller ungefär 2,38 Ω
Med 20 V som spänningen, dikterar Ohms Law att den totala strömmen är lika V / R, eller 20V / (43/18 ') = 360/43 A eller ungefär 8,37 A. Med denna totala ström kan du bestämma spänningsfallet över både R5 och R6 med Ohms Law (V = l / R) också.
För R5, V5 = 360/43 A x 5/6 Ω = 1800/258 V eller ungefär 6,98 V.
För R6, V6 = 360/43 A x 14/9 Ω = 1680/129 V eller ungefär 13.02 V.
Slutligen sjunker dessa spänningar för R5 och R6 kan delas tillbaka i de ursprungliga parallelliserade kretsarna för att beräkna ström av R1 och R2 för R5 och R2 och R3 för R6 använder Ohms Law.
I1 = (1800/258 V) / 1 '= 1800/258 A eller om 6,98 A._
I2 = (1800/258 V) / 5 '= 1500/43 A eller om 34,88 A._
I3 = (680/129 V) / 7 '= 4760/129 A eller ungefär 36,90 A.
I3 = (680/129 V) / 2 '= 1360/129 A eller ungefär 10,54 A.