En ellips kan definieras i plangeometri som uppsättningen av punkter så att summan av deras avstånd till två punkter (foci) är konstant. Den resulterande figuren kan också beskrivas icke-matematiskt som en oval eller "platt platta cirkel". Ellipser har ett antal tillämpningar inom fysik och är särskilt användbara för att beskriva planetbanor. Excentricitet är en av egenskaperna hos ellipsen och är ett mått på hur cirkulär ellipsen är.
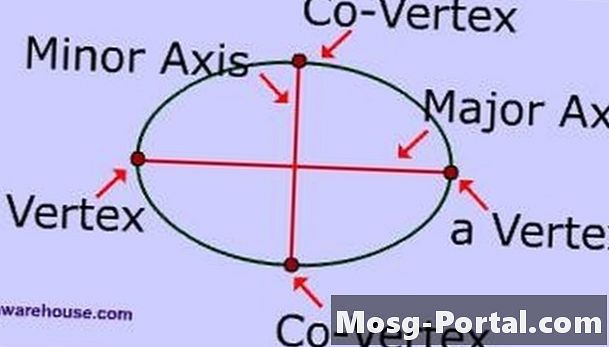
Undersök delar av en ellips. Huvudaxeln är det längsta linjesegmentet som korsar ellipsens centrum och har sina ändpunkter på ellipsen. Minoraxeln är det kortaste linjesegmentet som korsar ellipsens centrum och har sina ändpunkter på ellipsen. Huvudhalvaxeln är hälften av huvudaxeln och den mindre halvaxeln är halvan av mindre axeln.
Undersök formeln för en ellips. Det finns många olika sätt att beskriva en ellips matematiskt, men det mest användbara för att beräkna dess excentricitet är för en ellips är följande: x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1. Konstanterna a och b är specifika för en viss ellips och variablerna är x- och y-koordinaterna för punkter som ligger på ellipsen. Denna ekvation beskriver en ellips med dess centrum vid ursprunget och större och mindre axlar som ligger på x- och y-ursprunget.
Identifiera längden på halvaxlarna. I ekvationen x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1, anges längden på halvaxlarna med a och b. Det större värdet representerar den stora halvaxeln och det mindre värdet representerar den mindre halvaxeln.
Beräkna placeringarna för fokuserna. Focierna finns på huvudaxeln, en på varje sida av mitten. Eftersom ellipsens axlar ligger på ursprungslinjerna kommer en koordinat att vara 0 för båda fokuserna. Den andra koordinaten för kommer att vara (a ^ 2 - b ^ 2) ^ (1/2) för en foci och - (a ^ 2 - b ^ 2) ^ (1/2) för den andra fokusen där a> b.
Beräkna ellipsens excentricitet som förhållandet mellan avståndet för ett fokus från centrum till längden på halv-huvudaxeln. Excentriciteten e är därför (a ^ 2 - b ^ 2) ^ (1/2) / a. Observera att 0 <= e <1 för alla ellipser. En excentricitet på 0 betyder att ellipsen är en cirkel och en lång, tunn ellips har en excentricitet som närmar sig 1.