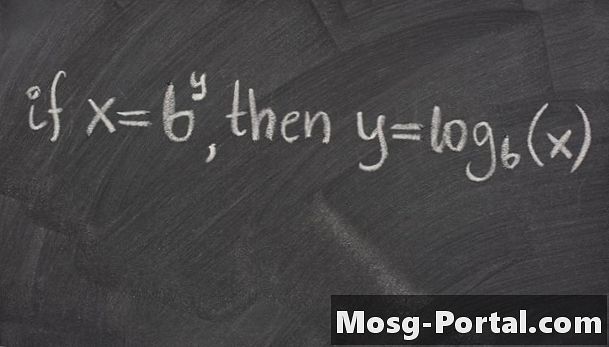
Innehåll
En logaritm är en matematisk funktion som är nära relaterad till exponentiella. I själva verket är logaritmen invers för den exponentiella funktionen. Den allmänna formen är log_b (x), som läser "log bas b av x." Ofta, log utan bas innebär bas 10 loggar log_10, och ln hänvisar till den "naturliga loggen," log_e, där e är ett viktigt transcendentalt nummer , e = 2.718282 .... I allmänhet, för att beräkna log_b (x), skulle du använda en räknare, men att känna till logaritmernas egenskaper kan hjälpa till att lösa speciella problem.
Egenskaper
Definitionen av en logaritmisk bas är log_b (b) = 1. Definitionen av den logaritmiska funktionen är om y = b ^ x, då log_b (y) = x. Några andra viktiga egenskaper är log_b (xy) = log_b (x) + log_b (y), log_b (x / y) = log_b (x) - log_b (y) och log_b (x ^ y) = ylog_b (x). Du kan använda dessa egenskaper för att hjälpa dig beräkna logaritmer i olika situationer.
Snabbtricks
Ibland kan du snabbt beräkna log_b (x) om du kan svara på problemet b ^ y = x. Log_10 (1 000) = 3 eftersom 10 ^ 3 = 1 000. Log_4 (16) = 2 eftersom 4 ^ 2 = 16. Log_25 (5) = 0,5 eftersom 25 ^ (1/2) = 5. Log_16 (1/2) = -1/4 eftersom 16 ^ (- 1/4) = 1/2 eller (1/2) ^ 4 = 1/16. Med log_b (xy) -formel log_2 (72) = log_2 (8 * 9) = log_2 (8) + log_2 (9) = 3 + log_2 (9). Om vi uppskattar log_2 (9) ~ log_2 (8) = 3, då log_2 (72) ~ 6. Det verkliga värdet är 6,2.
Ändra baser
Anta att du känner log_b (x), men du vill veta log_a (x). Detta kallas att byta baser. Eftersom en ^ (log_a (x)) = x, kan du skriva log_b (x) = log_b. Med log_b (x ^ y) = ylog_b (x) kan du förvandla detta till log_b (x) = log_a (x) log_b (a). Genom att dela båda sidorna med log_b (a) kan du lösa för log_a (x): log_a (x) = log_b (x) / log_b (a). Om du har en kalkylator som baserar 10 loggar, men du vill veta log_16 (7.3), kan du hitta den genom log_16 (7.3) = log_10 (7.3) / log_10 (16) = 0.717.